View Transformation 视图变换
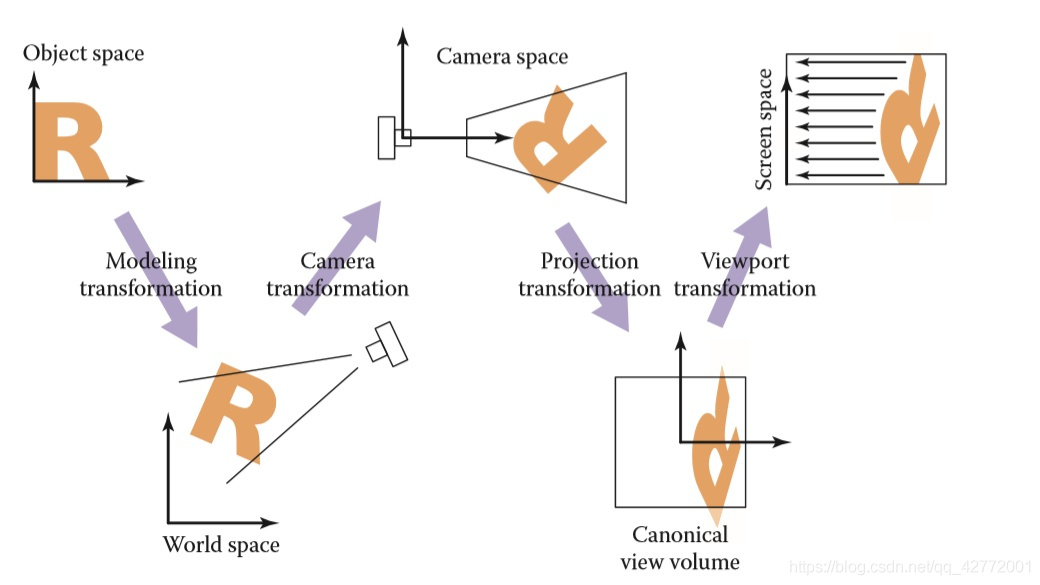
将虚拟世界中具有三维坐标的物体(x, y, z)变换到以二维的像素位置(x, y)来表示的屏幕坐标系之中:
-
模型变换 (modeling tranformation) 将场景中的物体调整至坐标所在位置
-
摄像机变换 (camera tranformation) 得到物体与摄像机的相对位置
-
投影变换 (projection tranformation) 便是根据平行投影或透视投影将三维空间投影至标准二维平面$[-1,1]^2$之上
-
视口变换 (viewport transformation) 将标准平面$[-1,1]^2$映射到屏幕分辨率范围$[0,width]*[0,height]$之内
1. Modeling tranformation 模型变换
利用基础的变换矩阵将世界当中的物体调整至我们想要的地方
-
基础变换/仿射变换 = 线性变换 + 平移
-
线性变换 = 旋转 + 缩放 + 切变
2. Camera tranformation 摄像机变换
把摄像机的坐标轴(假设为u,v,w分别对应原世界空间中的x,y,z)移动到标准的x,y,z轴
定义以下几个变量: 相机或眼睛位置 (eye postion):$\boldsymbol{e}$ 观察方向 (gaze postion):$\boldsymbol{g}$ 视点正上方向 (view-up vector): $\boldsymbol{t}$
摄像机坐标系定义如下:
\[\boldsymbol{w}=-\frac{\boldsymbol{g}}{\|\boldsymbol{g}\|} , \boldsymbol{u}=\frac{\boldsymbol{t} \times \boldsymbol{w}}{\| \boldsymbol{t} \times \boldsymbol{w}\|} , \boldsymbol{v}= \boldsymbol{w} \times \boldsymbol{u}\]将摄像机坐标移动到原坐标系:
\[M_{cam} = \begin{bmatrix} \boldsymbol{u} & \boldsymbol{v} & \boldsymbol{w} & \boldsymbol{e} \\ 0 & 0 & 0 & 1 \end{bmatrix} ^ {-1}\]
3. Projection tranformation 投影变换
3.1 Orthographic projection 正交投影
正交投影将将物体转换到一个$[-1,1]^2$的正方体中。
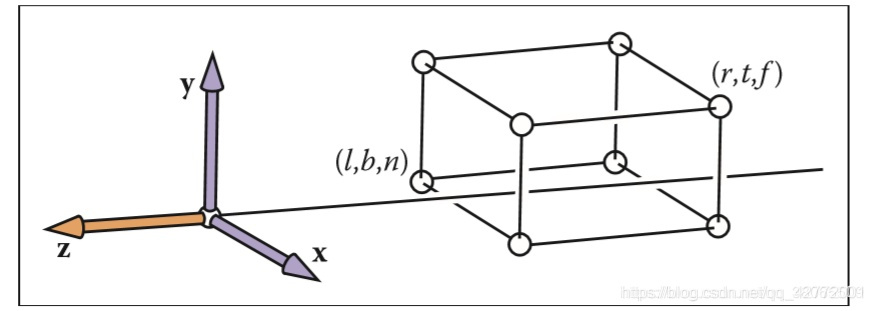
首先定义:
\[\begin{aligned} &x=l\equiv left \ plane \\ &x=r\equiv right \ plane \\ &y=b\equiv bottom \ plane \\ &y=t\equiv top \ plane \\ &z=n\equiv near \ plane \\ &z=f\equiv far \ plane \end{aligned}\]空间转换分为三个步骤,
- 将原空间范围的左下角移至原点
- 缩放给定倍数
- 将缩放后的空间范围移至新空间范围
以二维转换为例:
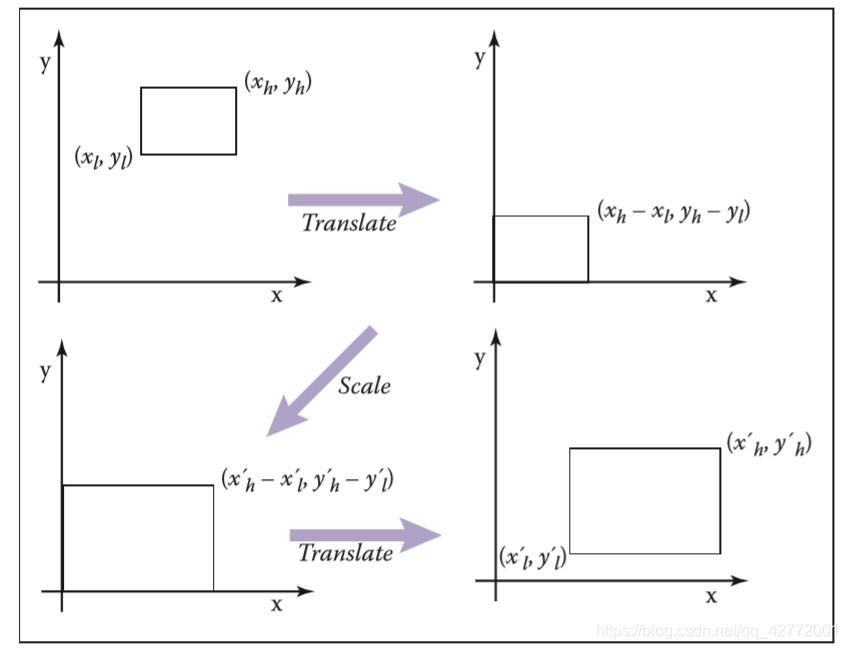
可以得到变换矩阵:
\[\begin{aligned} window&=translate(x_l',y_l')\ scale(\frac{x_h'-x_l'}{x_h-x_l},\frac{y_h'-y_l'}{y_h-y_l}) \ translate(-x_l,-y_l) \\ &=\begin{bmatrix} 1 & 0 & x_l' \\ 0 & 1 & y_l' \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{x_h'-x_l'}{x_h-x_l} & 0 & 0 \\ 0 & \frac{y_h'-y_l'}{y_h-y_l} & 0 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & -x_l \\ 0 & 1 & -y_l \\ 0 & 0 & 1 \end{bmatrix} \\ &=\begin{bmatrix} \frac{x_h'-x_l'}{x_h-x_l} & 0 & \frac{x_l'x_h-x_h'x_l}{x_h-x_l} \\ 0 & \frac{y_h'-y_l'}{y_h-y_l} & \frac{y_l'y_h-y_h'y_l}{y_h-y_l} \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}\]推广到三维:
\[\begin{bmatrix} \frac{x_h'-x_l'}{x_h-x_l} & 0 & 0 & \frac{x_l'x_h-x_h'x_l}{x_h-x_l} \\ 0 & \frac{y_h'-y_l'}{y_h-y_l} & 0 & \frac{y_l'y_h-y_h'y_l}{y_h-y_l} \\ 0 & 0 & \frac{z_h'-z_l'}{z_h-z_l} & \frac{z_l'z_h-z_h'z_l}{z_h-z_l} \\ 0 & 0 & 0 &1 \end{bmatrix} \\\]代入数据,可得到正交投影矩阵$M_{orth}$如下:
\[M_{orth}=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 &1 \end{bmatrix} \\\]3.2 Perspective Projection 透视投影
可以看作是先从透视转换到正交,即先把左边的frustum压缩成右边的cuboid形状,再应用正交投影中的$M_{orth}$矩阵:
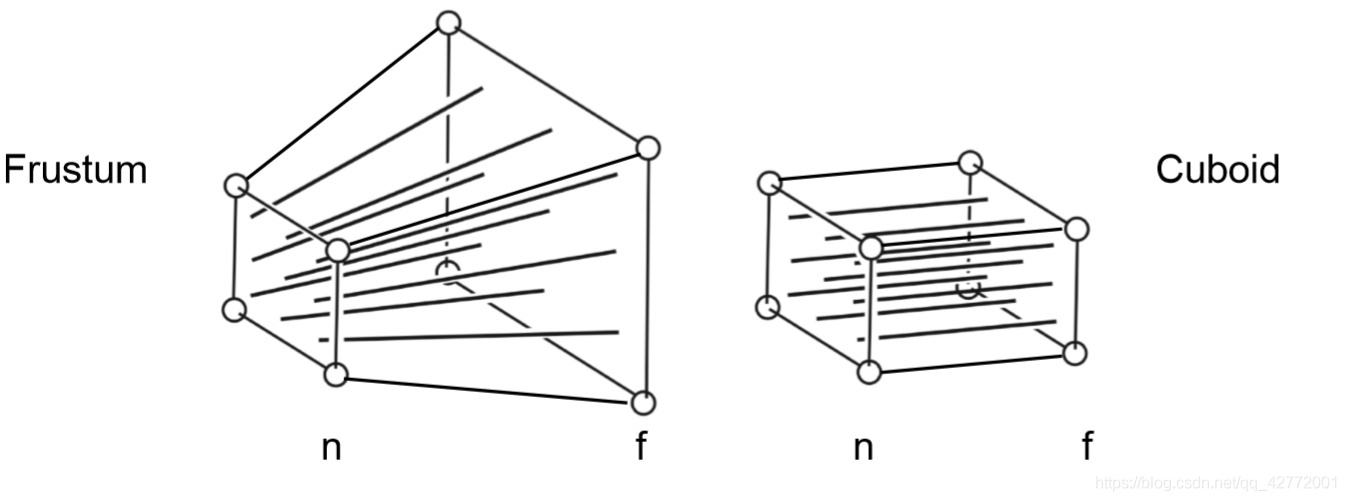
可以用相似三角形来解释:
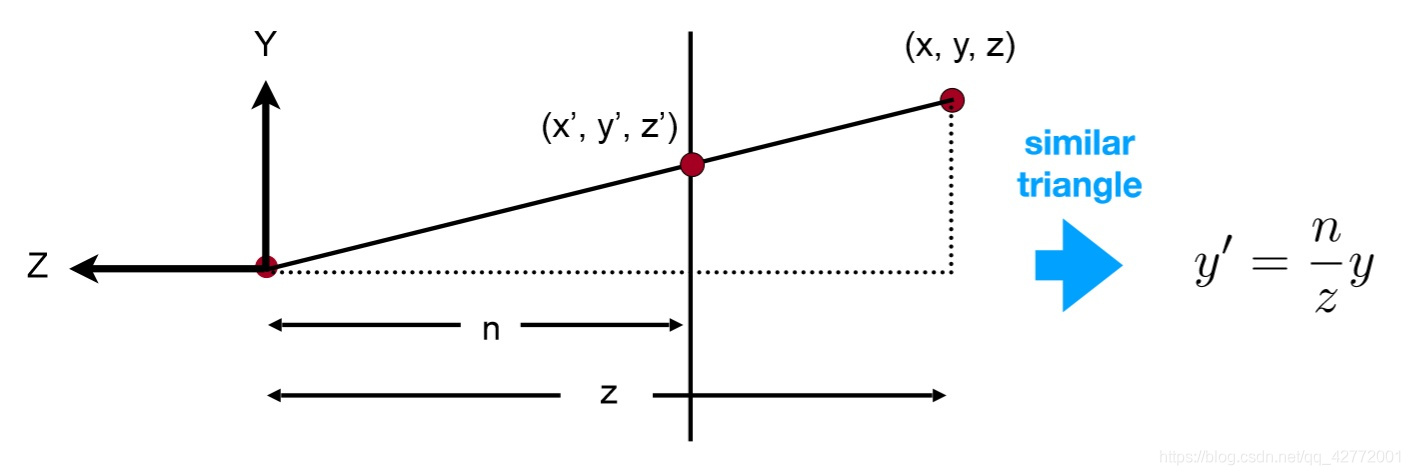
参考这篇对投影矩阵的解释:
得到的初步变换矩阵:
\[\begin{aligned} M_{persp→ortho}=\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -fn \\ 0 & 0 & 1 & 0 \end{bmatrix} \end{aligned}\]将它与正交投影矩阵相乘,可以得到透视投影矩阵:
\[\begin{aligned} M_{per}&=M_{ortho}M_{persp→ortho} \\ &=\begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0 \\ 0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0 \\ 0 & 0 & \frac{f+n}{n-f} & \frac{2fn}{f-n} \\ 0 & 0 & 1 & 0 \end{bmatrix} \end{aligned}\]
4. Viewport tranformation 视口变换
把标准立方体$[-1,1]^2$转换到屏幕空间$[0,width]*[0,height]$上:
\[M_{viewport}=\begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 &1 \end{bmatrix} \\\]
5. Summary 总结
把四个变换总结起来得到最后的变换:
\[M=M_{view}M_{per}M_{cam}M_{model}\]