Effective Water Simulation from Physical Models
Links:
Chapter 1. Effective Water Simulation from Physical Models
本章是关于在GPU中模拟大水体的系统,结合了基本网格几何波动和动态法线贴图生成,适用于实时游戏。
由计算简单的正弦函数之和对水面进行近似模拟开始,逐步扩展到更复杂的函数如Gerstner波,也扩展到像素着色器。主要思路是使用周期波的加和,来创建动态的平铺(tiling)凹凸贴图,从而获得优质的水面细节。
1. The Sum of Sines Approximation
需要运行两个表面模拟:一个用于表面网格的几何波动,另一个是网格上法线图的扰动。两个模拟本质上是相同的。
水面高度由简单的周期波叠加表示。正弦函数叠加后得到一个连续函数,这个函数描述了水面上所有点的高度和方向。在处理顶点时,基于每个顶点的水平位置对函数取样,使得网格细分形成连续水面。在几何分辨率之下,将该技术继续应用于纹理空间。通过对近似正弦叠加的法线取样,用简单像素着色器渲染到渲染目标纹理(render target texture),从而产生表面的法线图。对每帧渲染法线图,允许有限数量的正弦波组相互独立地运动,大大提高了渲染的逼真度。
1.1 波的选择
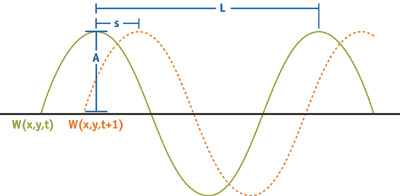
对于每个波的组成,有如下几个参数需要选择:
- 波长Wavelength (L):世界空间中波峰到波峰之间的距离。波长$L$与角频率$ω$的关系为$ω=2π/L$。
- 振幅Amplitude (A):从水平面到波峰的高度。
- 速度Speed (S):每秒种波峰移动的距离。为了方便,把速度表示成相位常数$φ=S\times 2π/L$。
- 方向Direction (D):垂直于波峰沿波前进方向的水平矢量。
波的状态定义为水平位置$(x,y)$和时间$t$的函数:
\[W_i(x,y,t)=A_i\times sin(\textbf{D}_i \cdot(x,y)\timesω_i+t\timesφ_i)\]包括所有波$i$的总表面是:
\[H(x,y,t)=\sum(A_i \times sin(\textbf{D}_i \cdot (x,y)\times ω_i + t \timesφ_i))\]为了提供场景动力学的变量,我们将在约束中随机产生这些波的参数,随着时间的变化,我们会不断将某个波淡出,然后再以一组不同的参数将其淡入。且此过程的这些参数是相关联的,必须仔细地产生一套完整的参数组,才能使各个波以可信的方式进行组合。
1.2 Normals and Tangents 法线和切线
因为表面有定义明确的函数,所以可以直接计算任意给定点处的曲面方向,而不是依赖于有限差分技术。
副法线(Binormal)$\textbf{B}$和正切矢量$\textbf{T}$分别是x和y方向上的偏导数。对于2D水平面中的任意点$(x,y)$,表面上的三维位置$\textbf{P}$为:
\[\textbf{P}(x,y,t)=(x,y,H(x,y,t))\]求副法线$\textbf{B}$方向,即对上式对x方向求偏导;而求正切矢量$\textbf{T}$方向,即对上式对y方向求偏导。
法线$\textbf{N}$由副法线$\textbf{B}$和切线$\textbf{T}$的叉积给出:
\[\textbf{N}(x,y)=\textbf{B}(x,y) \times \textbf{T}(x,y)\]直接叠加正弦波产生的波浪有很多roll(?),实际中的波峰比较尖,波谷比较宽,用正弦函数的变形可以达到这种效果,将正弦函数修改为非负然后加上指数k:
\[W_i(x,y,t)=2A_i\times \left( \frac{sin(\textbf{D}_i \cdot(x,y)\times ω_i+t \times φ_i)+1}{2} \right)^k\] \[\frac{\partial}{\partial x}(W_i(x,y,t))=k \times \textbf{D}_i \cdot x \times ω_i \times A_i \times \left( \frac{sin(\textbf{D}_i \cdot(x,y)\times ω_i+t\timesφ_i)+1}{2} \right)^{k-1} \\ \times cos( \textbf{D}_i \cdot (x,y) \times ω_i + t \times φ_i )\]下图展示了改变k产生的波形。
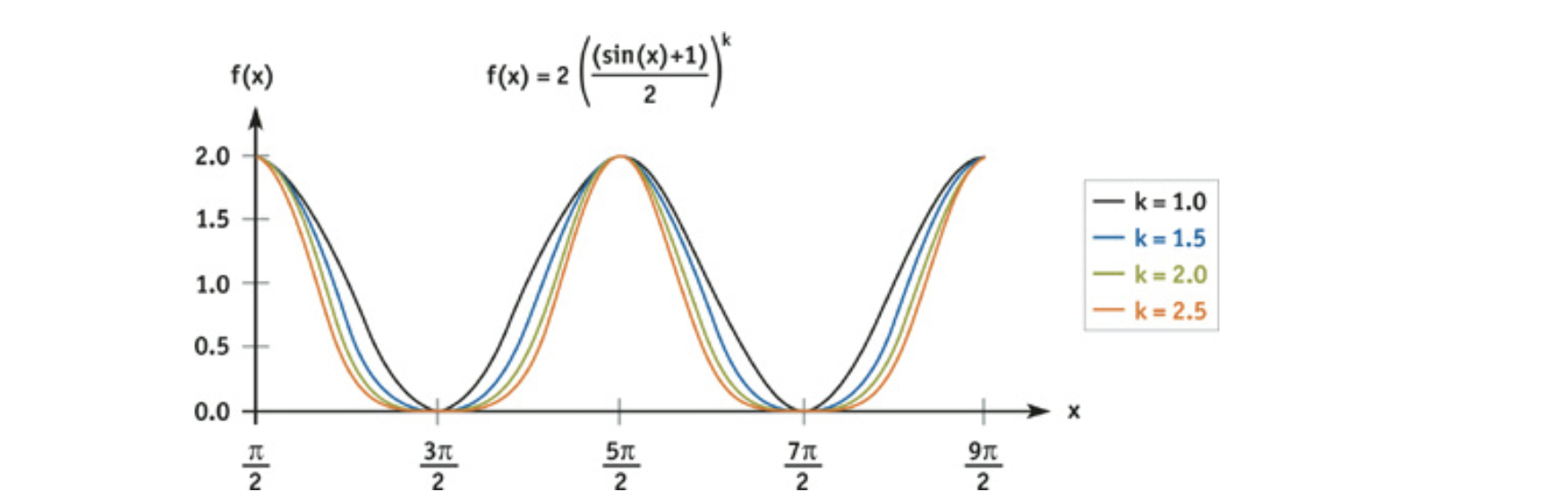
1.3 Geometric Waves 几何波
将几何波限制为4个,因为添加更多的波并不能增加新的概念,只不过增加更多相同的顶点Shader处理指令和常数而已。
1.3.1 Directional or Circular 方向/圆形波
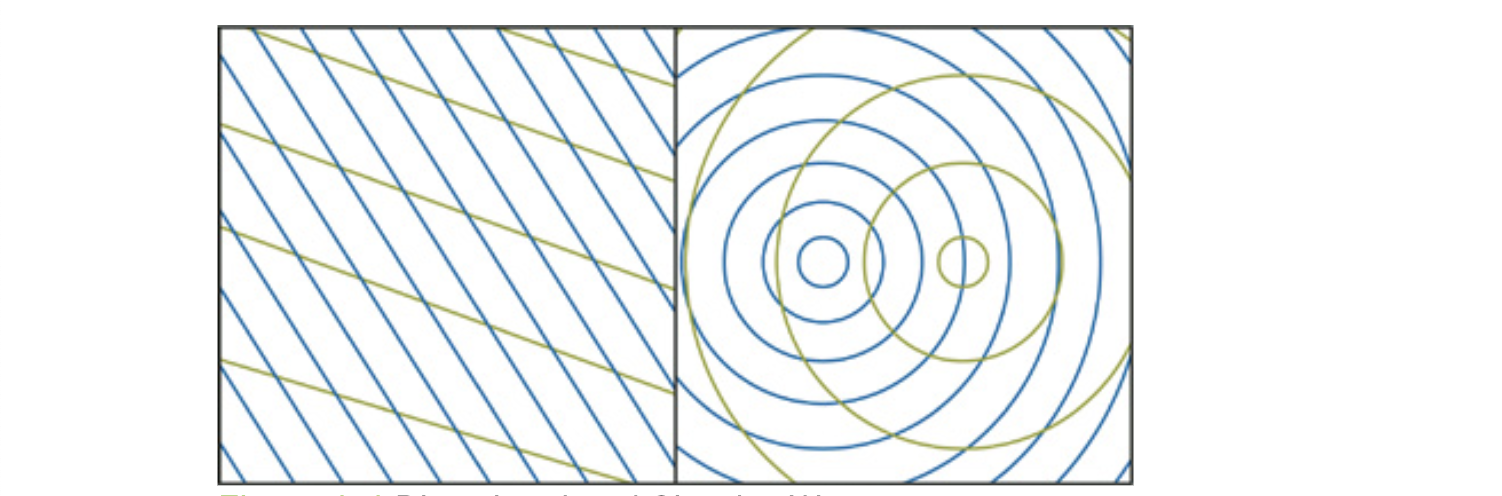
对于两种类型的波,视觉特性和复杂性都是由干涉条纹引起的。
方向波需要的顶点shader处理指令较少,但是究竟选择何种波需要取决于模拟的场景。对于大的水体,方向波往往更好,因为它们是风吹动产生的波较好的模型。对于较小的池塘的水,产生波的原因不是由于风,而是诸如例如瀑布,水中的鱼,圆形波则更好一些。对于方向波,波的方向是在风向的一定范围内任意绘制的;对于圆形波,波中心是在某些限定的范围内任意绘制的。
1.3.2 Gerstner Waves
正弦波看起来圆滑,用于渲染平静池塘一类的水体;而对于粗犷的海洋,需要形成较尖的浪头和较宽的浪槽,则可以选择Gerstner波。
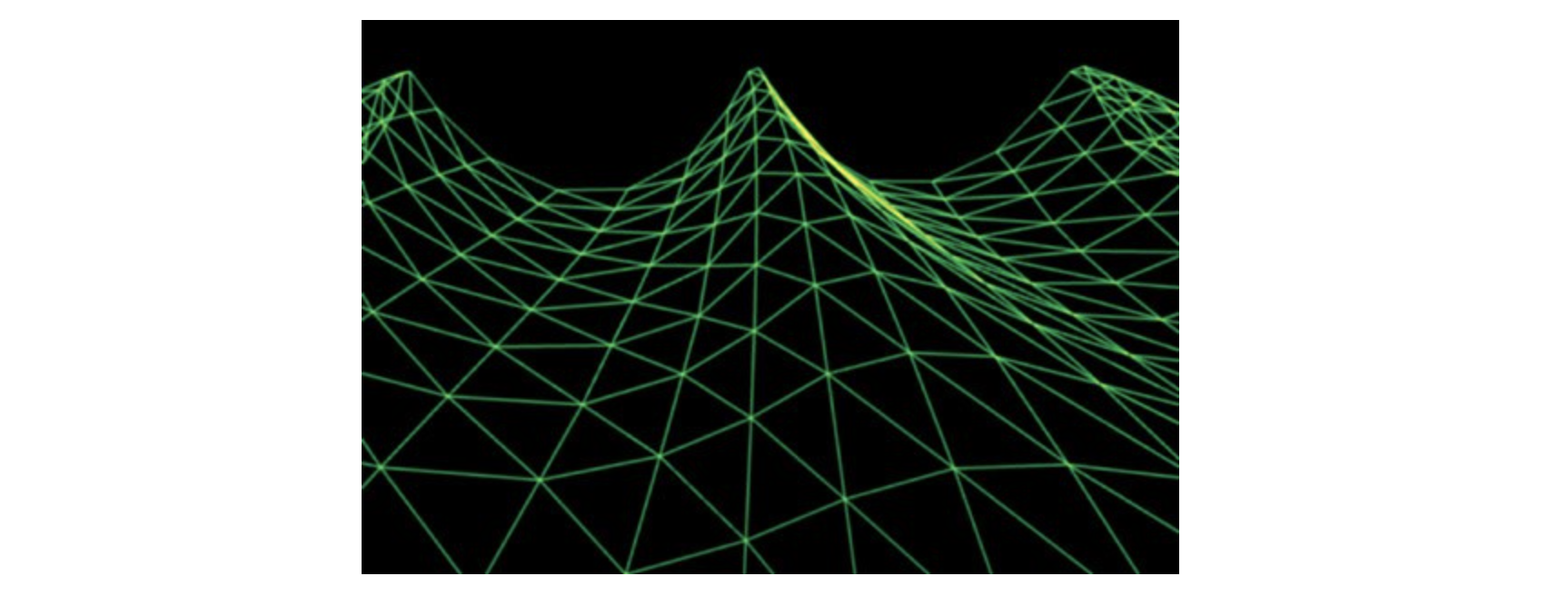
1.3.3 波长等参数选择
-
波长
要点是不追求波在真实世界中的分布,而是要使用现在的少数几个波达到最大效果。对波长相似的波进行叠加可以突显水面的活力。于是文中选择中等的波长,然后从它的1/2至两倍之间产生任意波长。
-
波速
基于波长的公式,忽略高次项的水的传播关系计算:$ω=\sqrt{g \times \frac{2\pi}{L}}$
-
振幅
主要是在Shader中指定一个系数,由美术人员对波长指定对应的合适振幅。
-
方向
运动方向与其他参数完全独立,因此可以自由选择。