Transforms 数学相关
这是《Real-time Rendering》的笔记系列第四章:Transform。
1. 基础变换 Basic Transforms
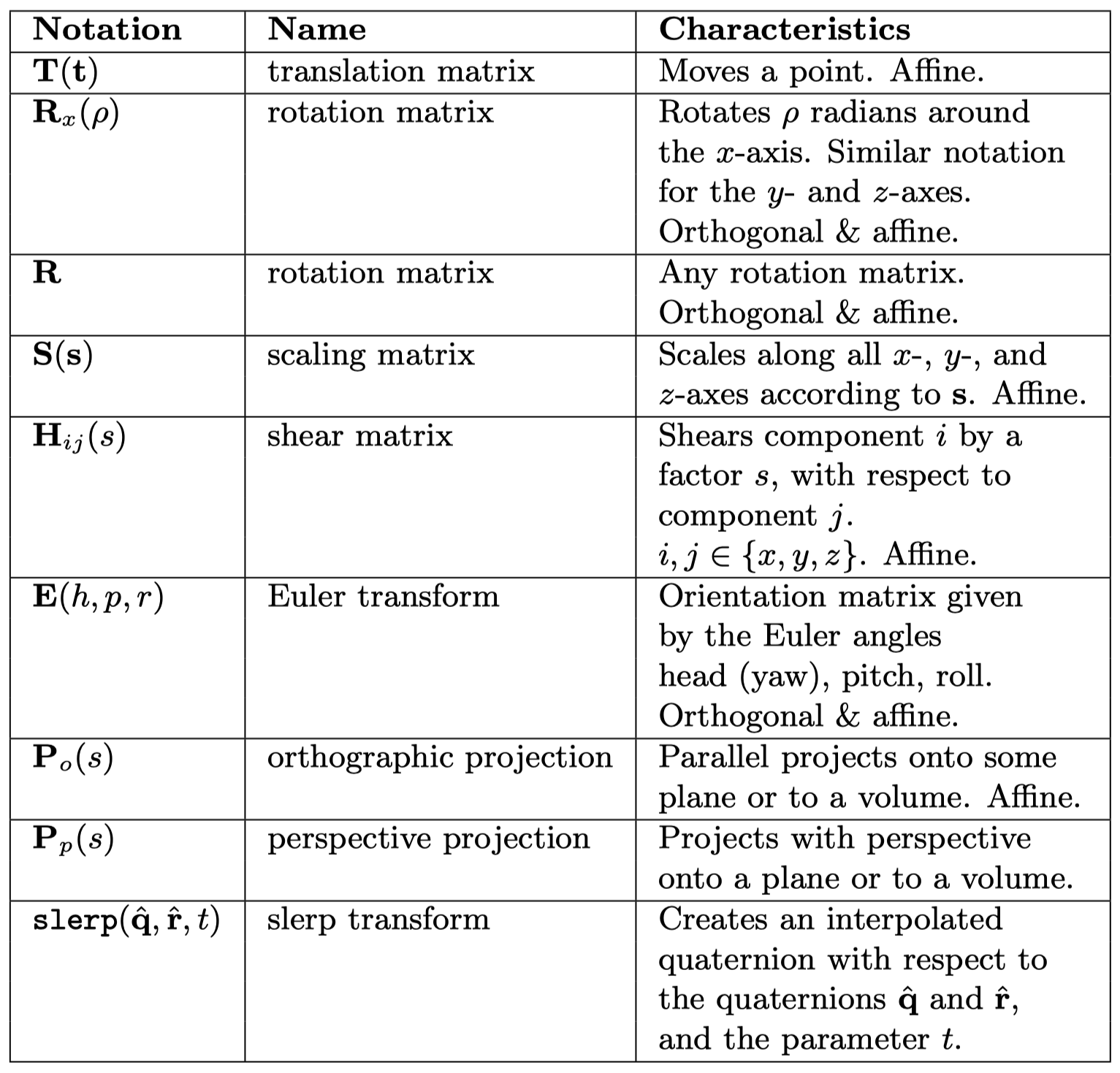
1.1 Translation 平移
用一个变换矩阵$\textbf{T}$来表示一个位置到另外一个位置的平移:
\[\textbf{T}(\textbf{t})=\textbf{T}(t_x,t_y,t_z)= \begin{pmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{pmatrix}\]平移变换的逆是${\textbf{T}}^{-1}(\textbf{t})=\textbf{T}(-\textbf{t})$,即向量$\textbf{t}$取反。注意一个方向向量$\textbf{v}=(v_x,v_y,v_z,0)$不会被$\textbf{T}$影响。
1.2 Rotation 旋转
三维中常用的旋转矩阵是$\textbf{R}_x(\phi)$、$\textbf{R}_y(\phi)$和$\textbf{R}_z(\phi)$,表示绕坐标轴旋转:
\[\textbf{R}_x(\phi)=\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & cos{\phi} & -sin{\phi} & 0 \\ 0 & sin{\phi} & cos{\phi} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\] \[\textbf{R}_y(\phi)=\begin{pmatrix} cos{\phi} & 0 & sin{\phi} & 0 \\ 0 & 1 & 0 & 0 \\ -sin{\phi} & 0 & cos{\phi} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\] \[\textbf{R}_z(\phi)=\begin{pmatrix} cos{\phi} & -sin{\phi} & 0 & 0 \\ sin{\phi} & cos{\phi} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]对任意轴的旋转会在2.4节里讨论。所有旋转矩阵的行列式都是1,而且是正交矩阵;另一种求逆方法是:${\textbf{T}}^{-1}(\textbf{t})=\textbf{T}(-\textbf{t})$,即沿相反方向旋转。
假设绕z轴旋转$\phi$弧度,旋转中心为某点$\textbf{p}$:
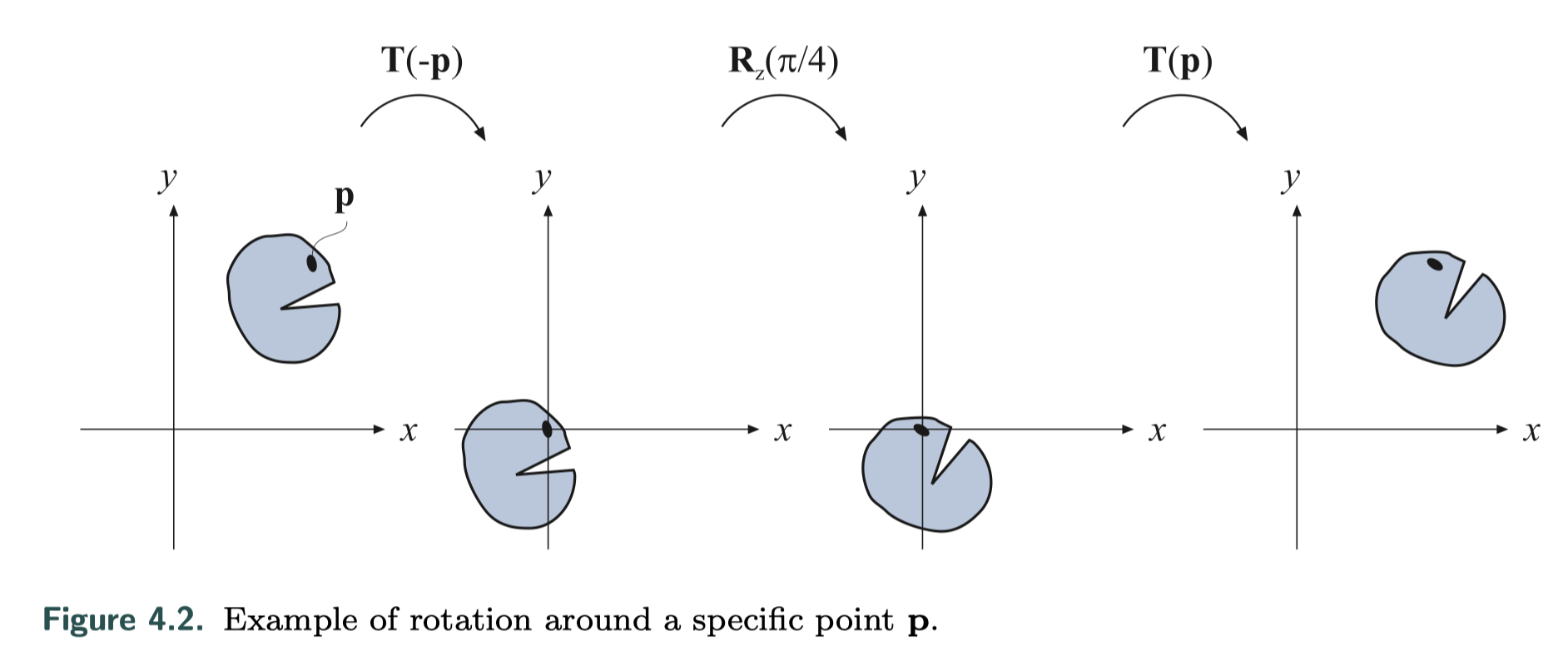
这个变换实际上可以视为用$\textbf{T}(\textbf{p})$平移对象$\textbf{p}$到原点,执行旋转$\phi$,再用$\textbf{T}(-\textbf{p})$平移回原始位置,得到的变换$\textbf{T}$如下式:
\[\textbf{X}=\textbf{T}(\textbf{p})\textbf{R}_z(\phi)\textbf{T}(-\textbf{p})\]1.3 Scaling 缩放
缩放变换矩阵$\textbf{S}(\textbf{s})$表示沿xyz轴分别缩放$s_x$、$s_y$和$s_z$因子:
\[\textbf{S}(\textbf{s})= \begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]如果$s_x=s_y=s_z$则缩放操作称为均匀的(uniform),否则为非均匀(nonuniform)操作,有时也使用等向性(isotropic)和各向异性(anisotropic)来形容。矩阵的逆用$\textbf{S}^{-1}(\textbf{s})=\textbf{S}(1/s_x,1/s_y,1/s_z)$表示。
使用齐次坐标,创建均匀缩放矩阵的另一种有效方法是通过操作位置$(3,3)$处的矩阵元素。该值会影响齐次坐标的w分量,因此会缩放矩阵转换后的点(非方向矢量)的每个坐标。例如,要均匀缩放5倍,可以将缩放矩阵中$(0,0)$、$(1,1)$、$(2,2)$的元素设置为5,或将$(3,3)$设置为$1/5$。执行此操作的两个不同矩阵如下所示:
\[\textbf{S}=\begin{pmatrix}5 & 0 & 0 & 0 \\0 & 5 & 0 & 0 \\0 & 0 & 5 & 0 \\0 & 0 & 0 & 1 \end{pmatrix}, \ \ \ \ \textbf{S}'=\begin{pmatrix}0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 1/5 \end{pmatrix}\]1.4 Shearing 错切/推移
错切变换可以用于扭曲整个场景来实现某些物理效果,或者扭曲单个物体的外观。例如一个变换$\textbf{H}_{xz}(s)$:
\[\textbf{H}_{xz}(s)=\begin{pmatrix}1 & 0 & s & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \end{pmatrix}\]参考3Blue1Brown的线代系列Essence of linear algebra,这个变换矩阵可以理解成原来z方向的单位分量变成了$(s,0,1)$如下图所示。
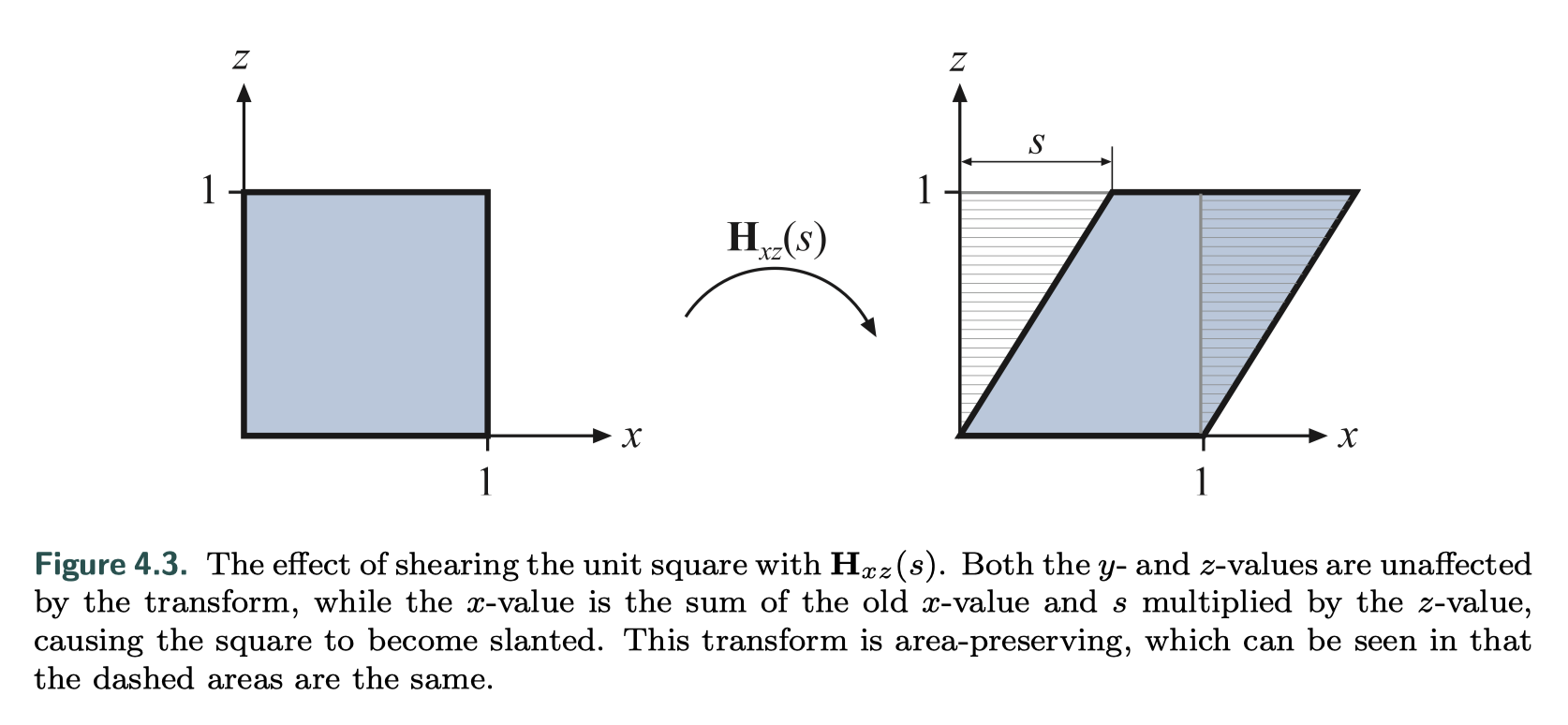
错切的逆变换是:
\[\textbf{H}_{ij}^{-1}(s)=\textbf{H}_{ij}(-s)\]如果是以下形式的变换:
\[\textbf{H}'_{xy}(s,t)=\begin{pmatrix}1 & 0 & s & 0 \\0 & 1 & t & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \end{pmatrix}\]实际上要表示的是
\[\textbf{H}’_{ij}(s,t)=\textbf{H}_{ik}(s) \textbf{H}_{jk}(t)\]任何错切变换矩阵的行列式都是1,从图中也可以知道错切是体积不变的变换。
1.5 Concatenation of Transforms 变换的级联
由于矩阵乘法的不可交换性,变换的级联被认为是顺序相关的。像下图的两种变换调转顺序,就会产生不一样的结果。
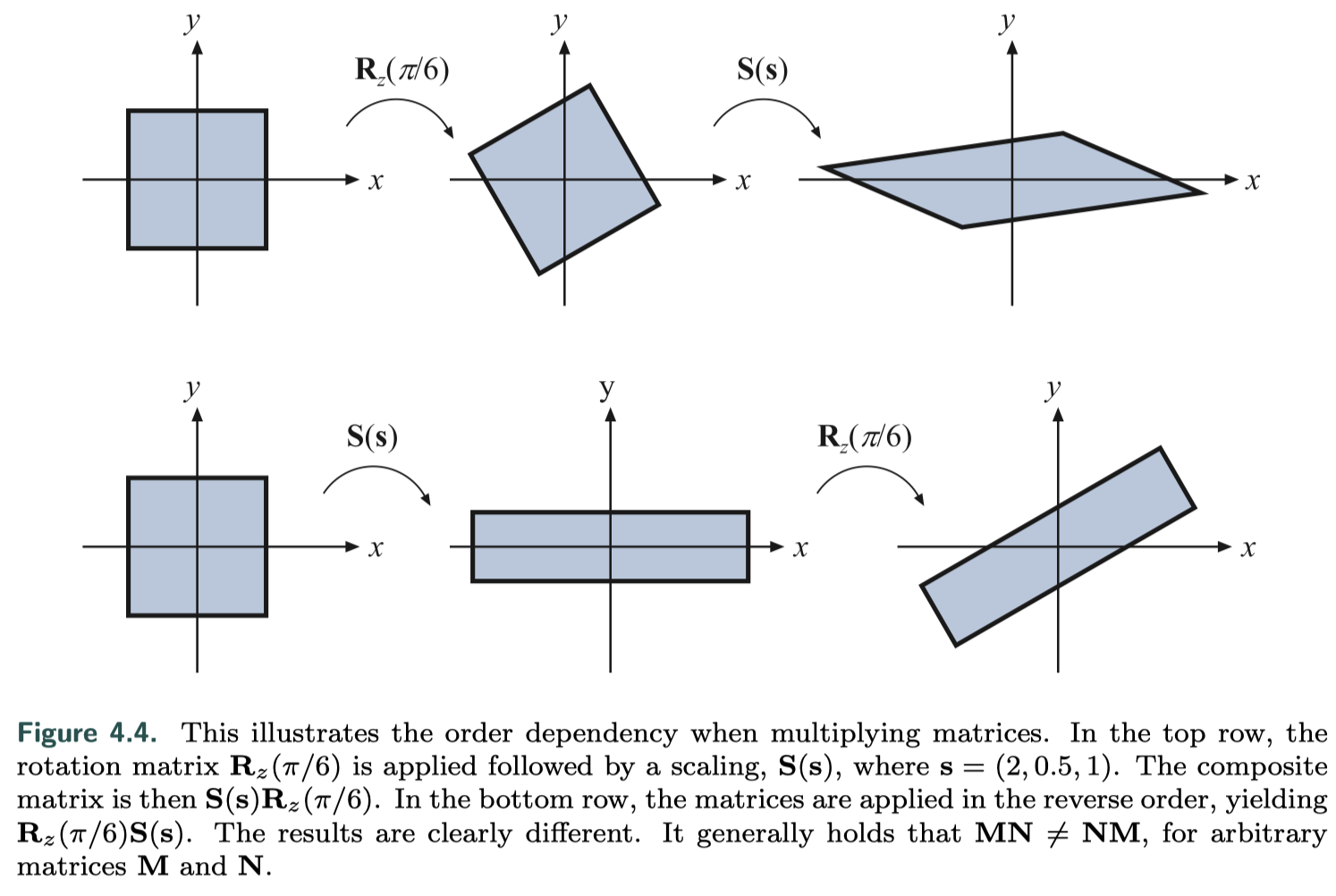
在实际应用中为了提高效率,会把所有变换连接到单个矩阵里,再对所有顶点进行处理。比如复合矩阵$\textbf{C}=\textbf{T}\textbf{R}\textbf{S}$,意味着$\textbf{T}\textbf{R}\textbf{S}\textbf{p}=(\textbf{T}(\textbf{R}(\textbf{S}\textbf{p})))$,即右边的缩放矩阵$\textbf{S}$最先应用于顶点$\textbf{p}$。另外,$\textbf{T}\textbf{R}\textbf{S}$是场景图形系统(?)中常用的顺序。
虽然矩阵级联依赖于顺序,但可以根据需要进行分组。比如用$\textbf{T}\textbf{R}\textbf{S}\textbf{p}$计算一次刚体变换$\textbf{T}\textbf{R}$,就可以分组成$(\textbf{T}\textbf{R})(\textbf{S}\textbf{p})$,使用中间结果。因此,矩阵级联是符合结合律(associative)的。
1.6 The Rigid-Body Transform 刚体变换
刚体变换指的是仅由平移和旋转组成的变换,它不影响物体的形状。任何刚体变换矩阵$\textbf{X}$都可以写作平移$\textbf{T}(\textbf{t})$和旋转$\textbf{R}$的级联:
\[\textbf{X}=\textbf{T}(\textbf{t})\textbf{R}=\begin{pmatrix}r_{00} & r_{01} & r_{02} & t_x \\r_{10} & r_{11} & r_{12} & t_y \\r_{20} & r_{21} & r_{22} & t_z \\ 0 & 0 & 0 & 1 \end{pmatrix}\]$\textbf{X}$的逆计算方法:
\[\textbf{X}^{-1}=(\textbf{T}(\textbf{t})\textbf{R})^{-1}=\textbf{R}^{-1}\textbf{T}(\textbf{t})^{-1}=\textbf{R}^T\textbf{T}(-\textbf{t})\]举例来说,一种常用的Orient camera操作就是刚体变换,比如OpenGL里的gluLookAt()函数。给定位于$\textbf{c}$的摄像机,原摄像机向上方向是$\textbf{c}’$,要朝向$\textbf{l}$的方向,需要计算出$\textbf{r}$,$\textbf{u}$和$\textbf{v}$。
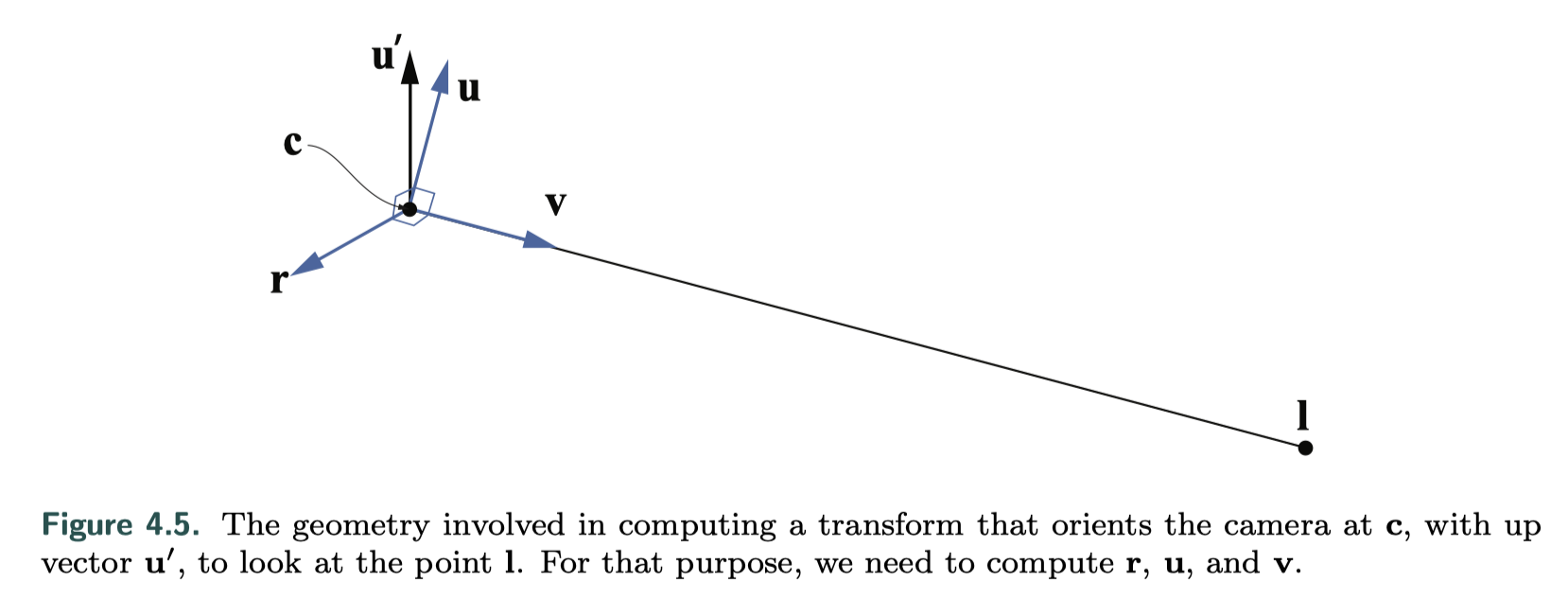
显而易见$\textbf{v}$用$\textbf{l}$和$\textbf{c}$就可以计算出来,接着用$\textbf{v}$和$\textbf{u}$叉乘得到$\textbf{r}$,注意这些计算都需要归一化。
1.7 Normal Transform 法线变换
直接对法线应用物体的变换矩阵会产生错误:
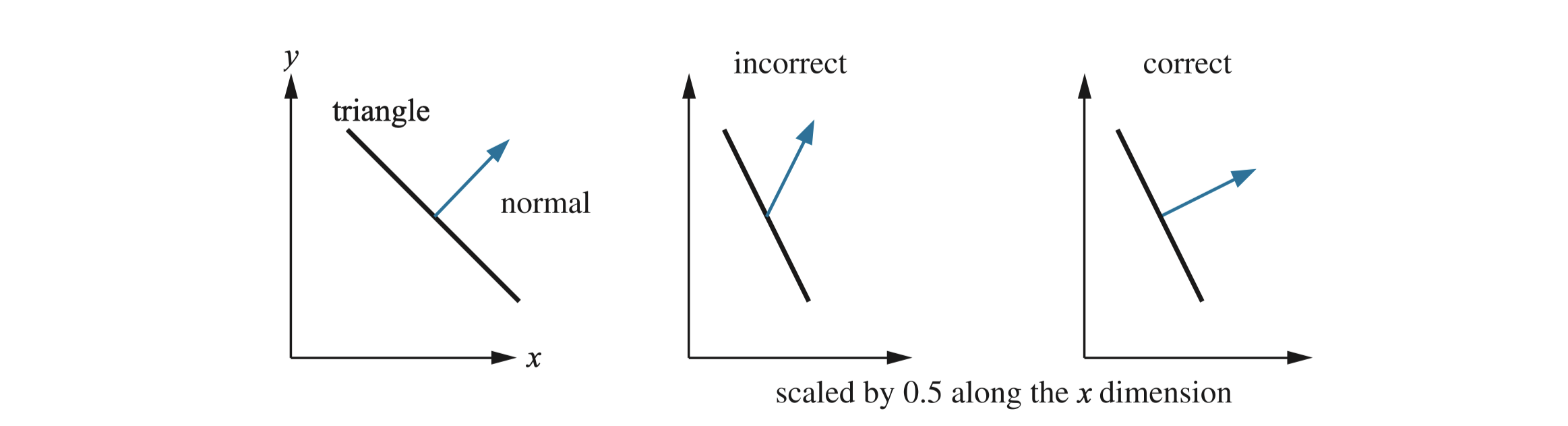
正确方法是使用伴随的转置,而不是乘以矩阵本身。实际比较常用的方法是计算逆的转置。逆是伴随矩阵除以原始矩阵的行列式,即,行列式为零的时候不能应用这种方法。
常见情况下,法线变换只需要计算左上角 3 × 3 分量的伴随。平移不影响法线,而且大多数建模变换都是仿射变换,不会改变w分量。
1.8 Computation of Inverses 逆的计算
三种计算逆的方式:
- 如果是一系列变换矩阵,可以采用反转参数的方法,即,如果原矩阵$\textbf{M}=\textbf{T}(\textbf{t})\textbf{R}(\phi)$,则逆是$\textbf{M}^{-1}=\textbf{R}(-\phi)\textbf{T}(-\textbf{t})$
- 对正交矩阵来说,$\textbf{M}^{-1}=\textbf{M}^T$
- 如果啥也不知道,就只能套公式的那些方法:伴随矩阵、Cramer 规则、LU 分解或高斯消元法。从架构上考虑,会选择前两种方法(if比较少)
2. Special Matrix Transforms and Operations 一些特殊变换
2.1 The Euler Transform 欧拉变换
2.2 Extracting Parameters from the Euler Transform
2.3 Matrix Decomposition
2.4 Rotation about an Arbitrary Axis
3. Quaternions 四元数
四元数的解释:
Visualizing quaternions (4d numbers) with stereographic projection - YouTube
对万向节死锁(gimbal lock)的解释:
Euler (gimbal lock) Explained - YouTube