Radiometry 辐射度量学
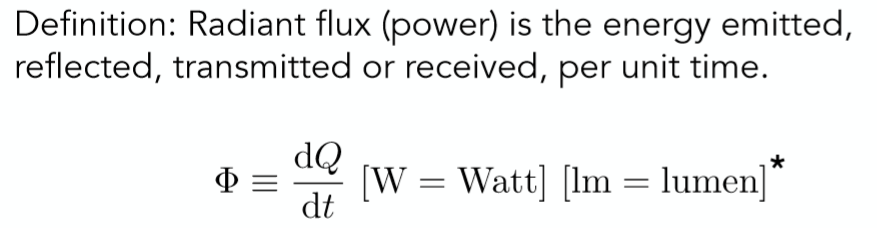
所谓辐射通量或者说辐射功率,其实就是在辐射能量的基础之上除以时间,也就是单位时间的能量。同样也可以用物理当中的功率来进行类比。
然后是这三个真的好乱的概念:
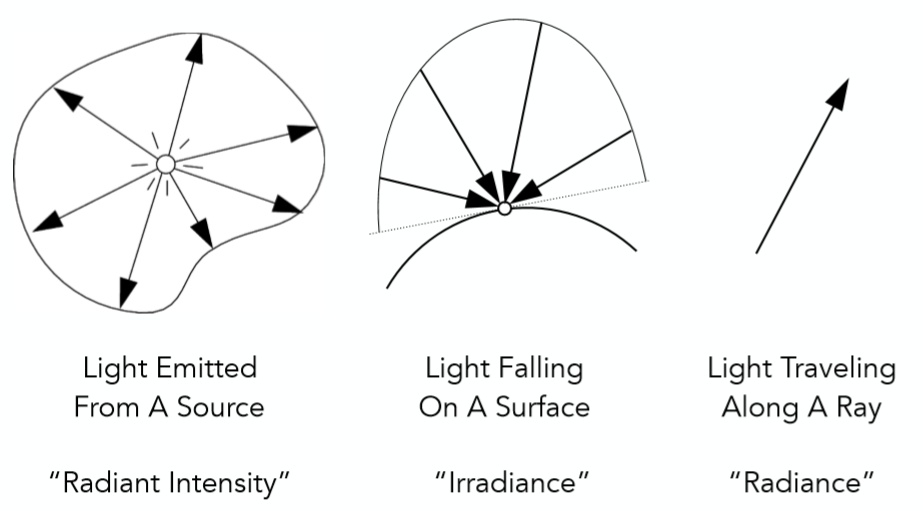
Radiant itensity其实就是指从一个光源出发某一方向上的亮度
Irradiance指某一微小平面所接受到的光线亮度
Radiance衡量的是一条传播光线所具有的亮度(不受传播方向影响而改变)
Radiant intensity 辐射强度
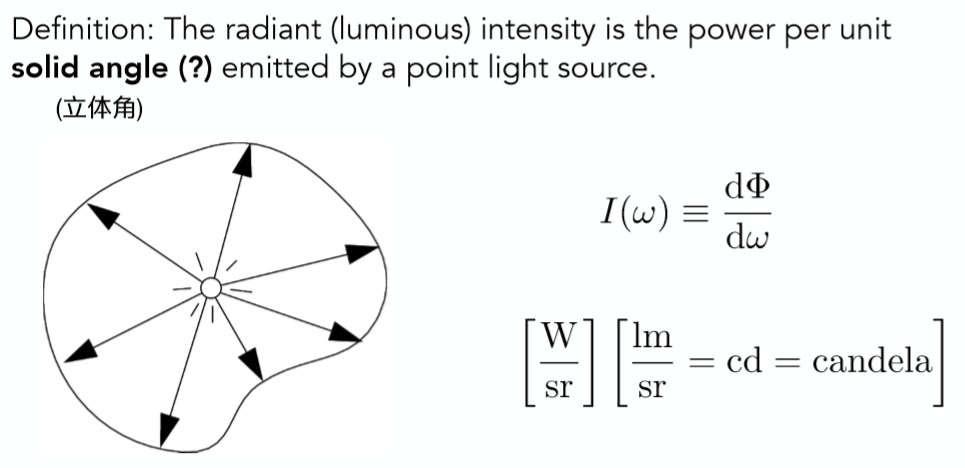
Radiant intensity一句话来说,就是从光源发出的每单位立体角(solid angle)上的功率。
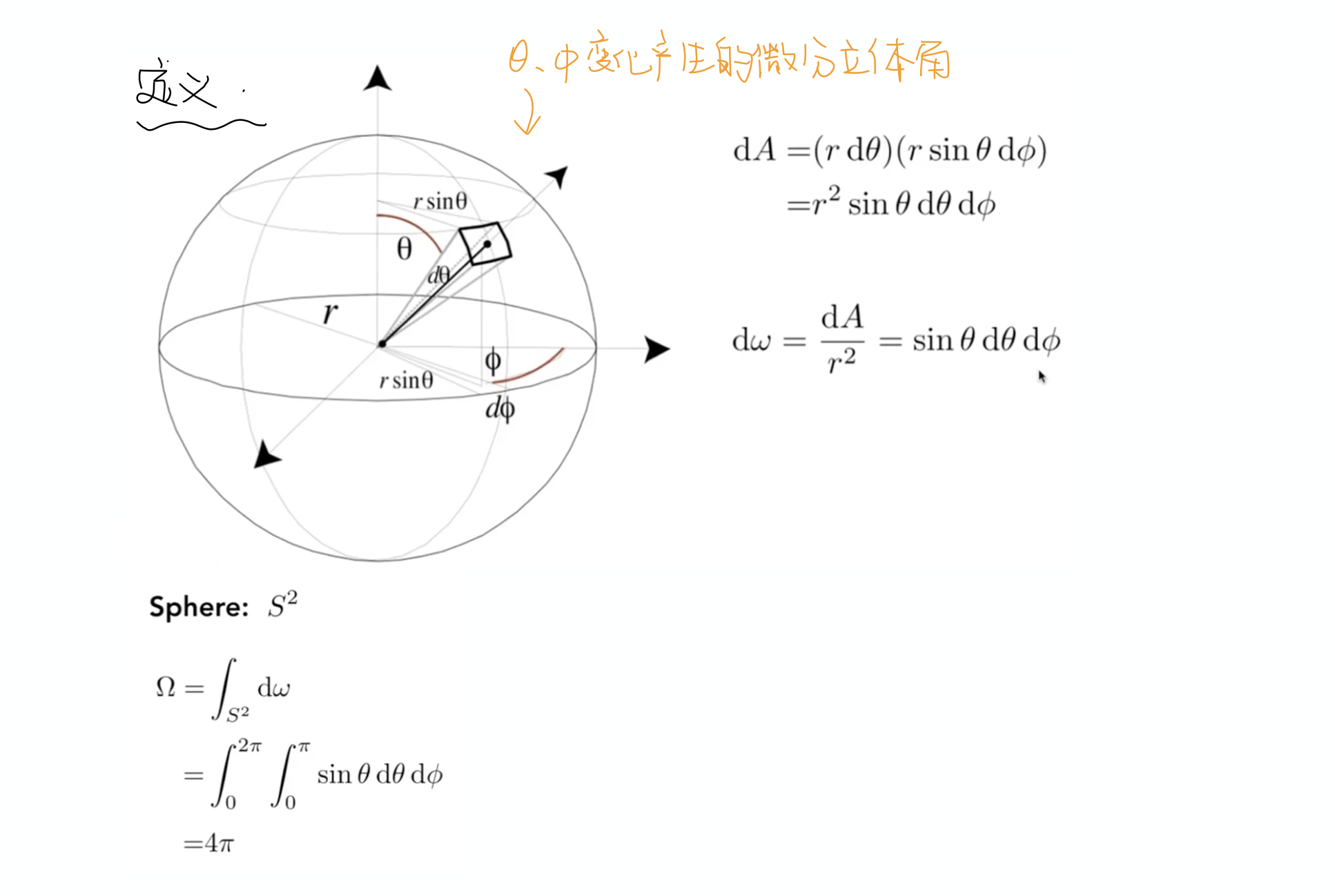
这里解释一下立体角,对应二维空间中圆的弧度在三维空间中球上的拓展:

即立体角度所对应球上的投影面积比上半径的平方,整个球的立体角为$4π$。
那么对于Radiant intensity的定义当中,微分立体角$dω$计算如下:
Irradiance 辐射照度

同样用一句话来说,irradiance是指每单位照射面积所接收到的power。
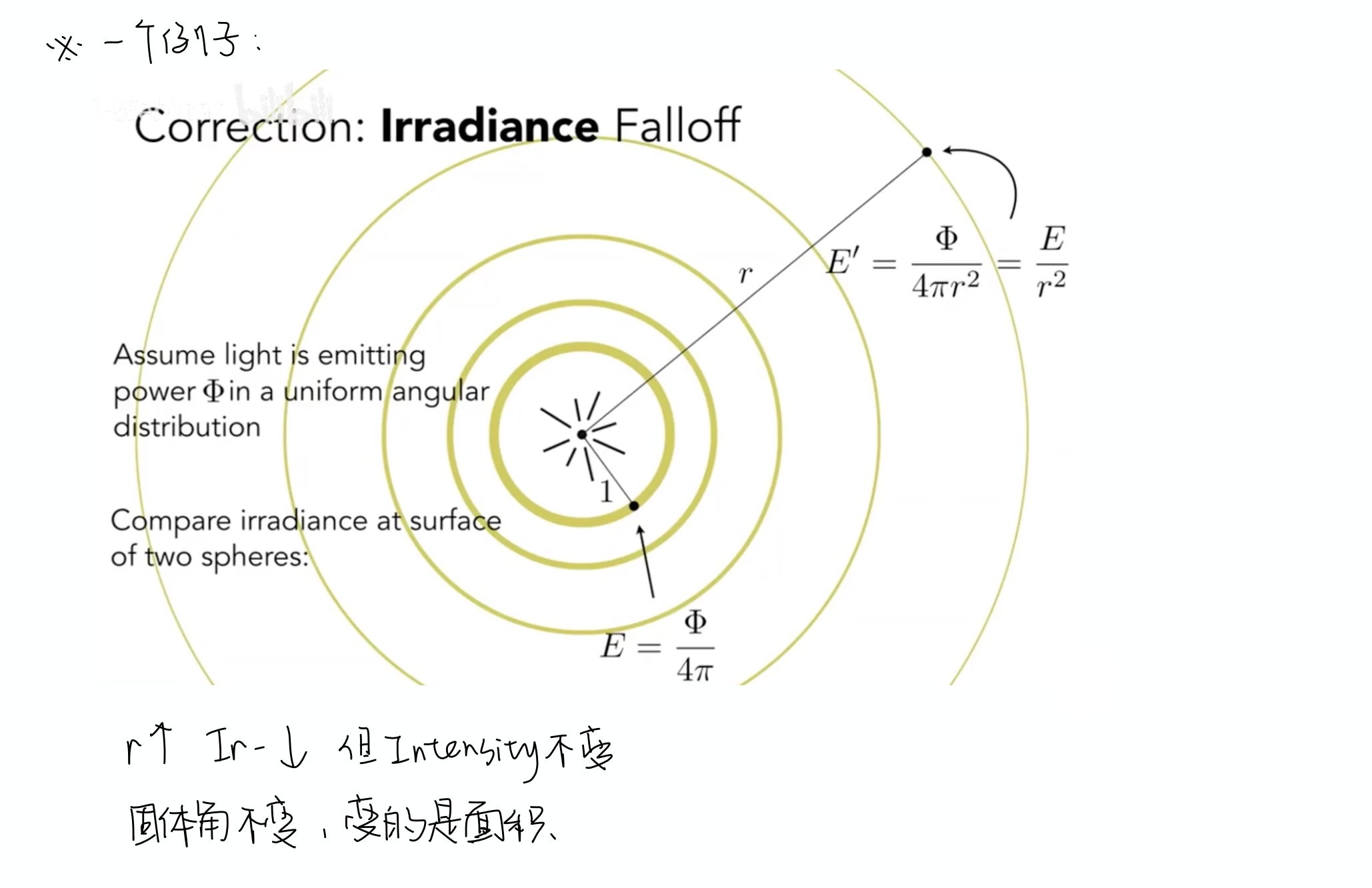
这个概念可以用来解释之前Blinn-Phong模型中乘以余弦值的原因,同样也可以解释光线越远越加衰减的例子:
Radiance 光亮度
所谓radiance就是指每单位立体角,每单位垂直面积的功率,直观来看的话,很像是Intensity和irradiance的结合,它同时指定了光的方向与照射到的表面所接受到的亮度。
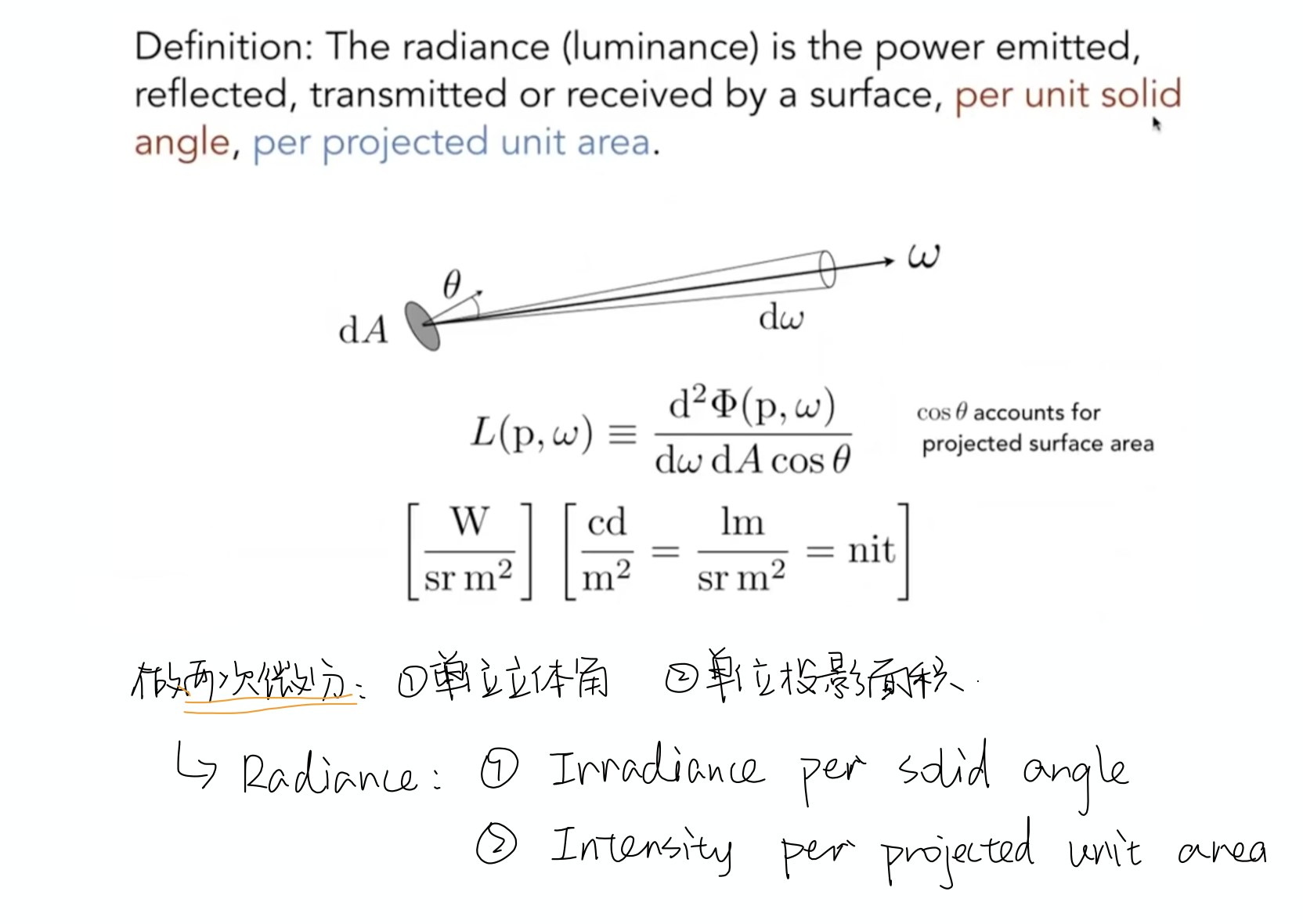
但这里有一个细微的区别,在irradiance中定义的每单位照射面积,而在radiance当中,为了更好的使其成为描述一条光线传播中的亮度,且在传播过程当中大小不随方向改变,所以在定义中关于接收面积的部分是每单位垂直面积,而这一点的不同也正解释了图中式子分母上的$cosθ$。
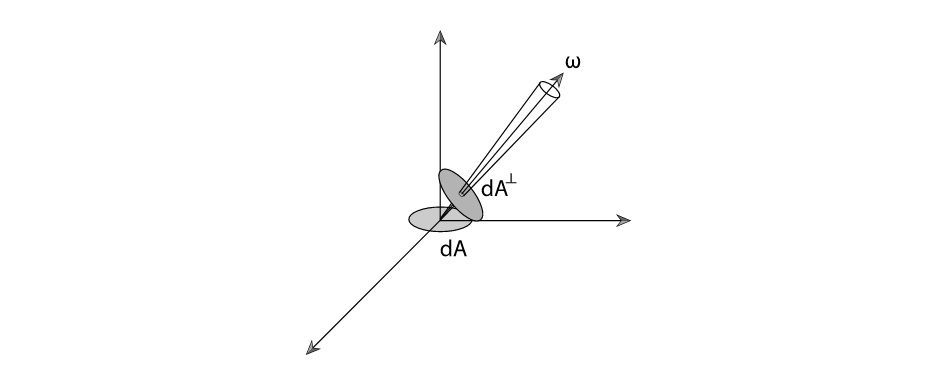
即图中的$dA$是irradiance中定义所对应的,而$dA^⊥$才是radiance中所定义的面积。二者之间的关系为$dA^⊥=dAcosθ$。
Irradiance & Radiance
由它们的定义:
\[L(p,ω)=\frac{dE(p)}{dωcosθ}\]进一步推导:
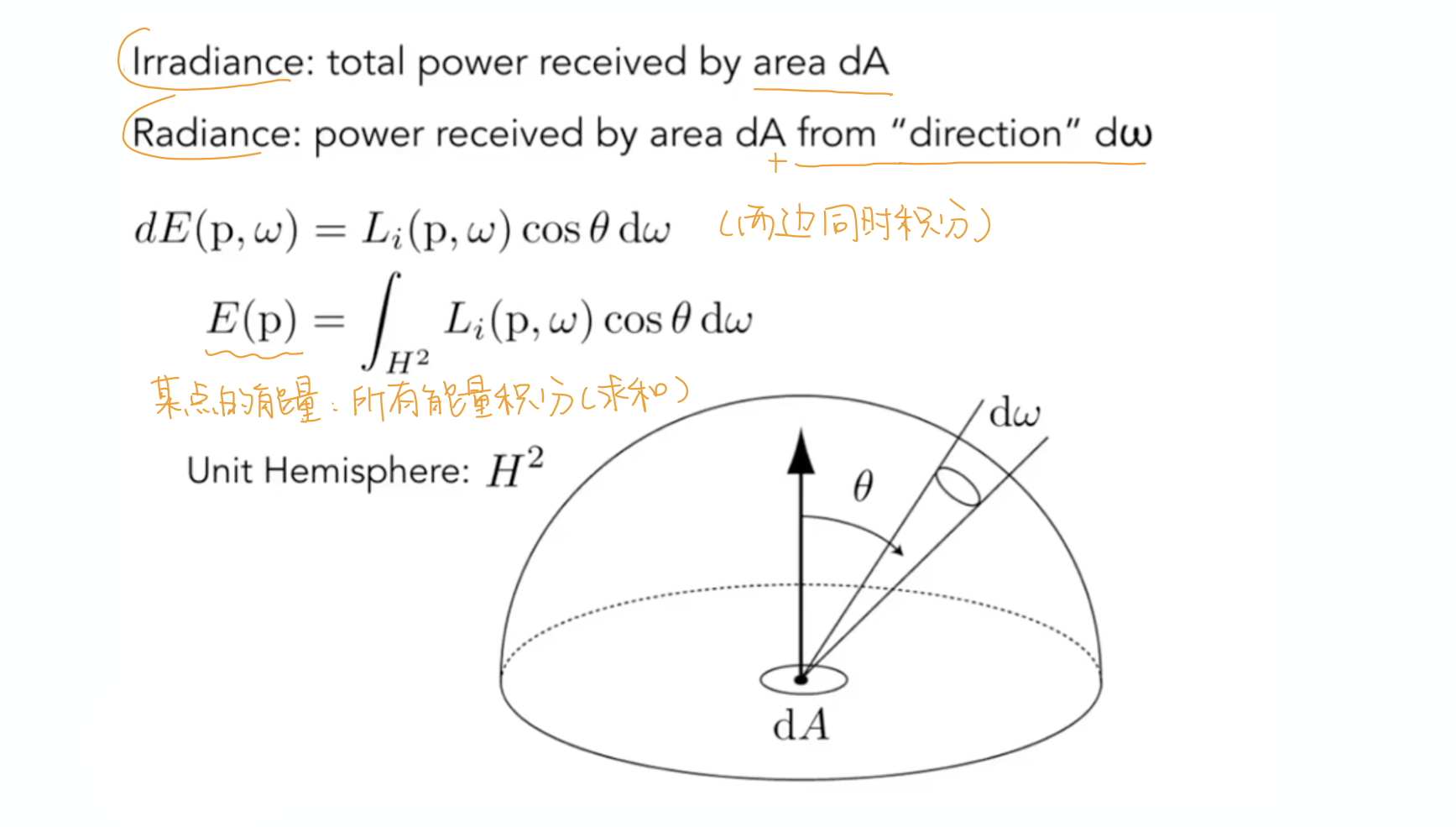
观察积分后的式子,$E(p)$就是点p的irradiance,其物理含义是上文所提到过的点p上每单位照射面积的功率,而$L_i(p,ω)$指入射光每立体角,每垂直面积的功率,因此积分式子右边的$cosθ$解释了面积上定义的差异,而对$dω$积分,相当于对所有不同角度的入射光线做一个求和。
该积分式子的物理含义便是,一个点(微分面积元)所接收到的亮度(irradiance),由所有不同方向的入射光线亮度(radiance)共同贡献得到。
BRDF 双向反射分布函数
利用辐射度量学,可以这样定义光的反射:

从直观的理解来说,不同物体表面材质自然会把一定方向上的入射亮度($dE(ω_i)$)反射到不同的方向的光线上($dL_r(ω_r)$)。比如理想光滑表面会把入射光线完全反射到镜面反射方向,其它方向完全没有;理想粗糙表面会把入射光线均匀的反射到所有方向。
因此所谓BRDF就是描述这样一个从不同方向入射之后,反射光线分布情况的函数,定义如下:
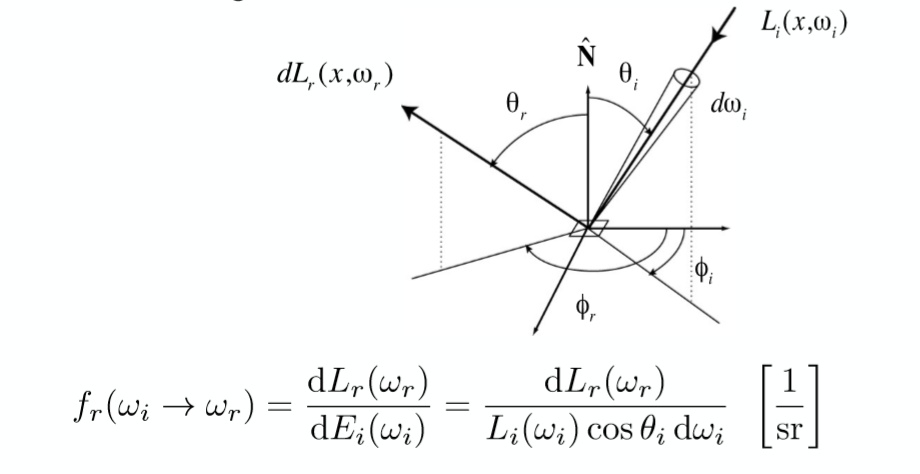
它接收两个参数,入射光方向$ω_i$,反射光方向$ω_r$,函数值为反射光的radiance与入射光的iiradiance的比值。(从某个方向接受到的光能有多少反射到另外一个方向)
The Reflection Equation 反射方程
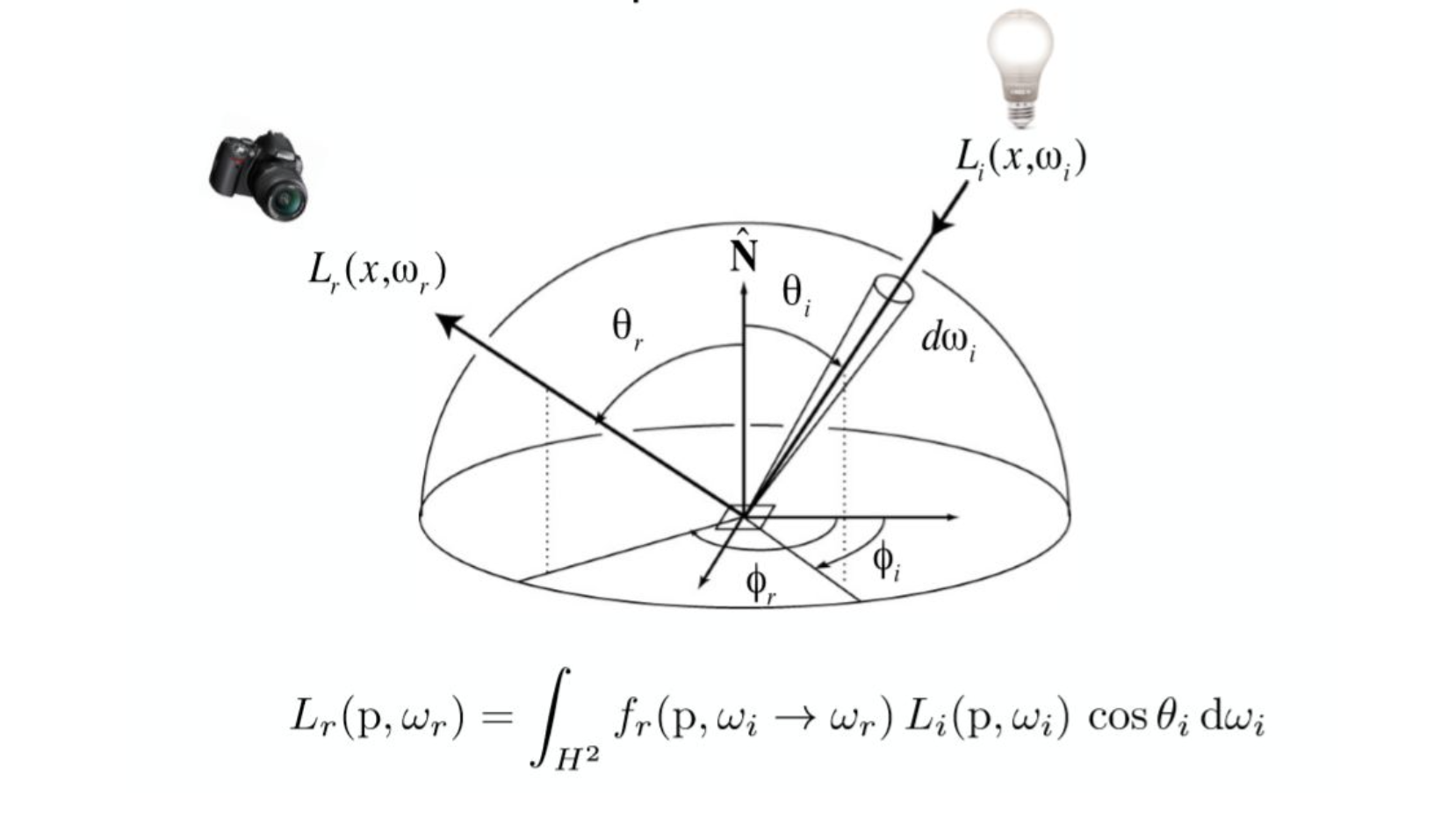
即摄像机所接受到的$ω_r$方向上的反射光,是由所有不同方向上入射光线的irradiance贡献得到的,而不同方向入射光线的irradiance对反射方向$ω_r$的贡献程度则由物体表面材质决定,所以乘上了一个BRDF函数。
入射光线的radiance不仅仅是光源所引起的,还有可能是其他物体上着色点的反射光线的radiance,恰好反射到当前的着色点p(即间接光照),同时其他物体上的反射光线的radiance依然也是由直接光照和间接光照构成,因此这与whitted-style当中的光线追踪过程十分类似,也是一个递归的过程。解方程比较难,在后面会写到。
The Rendering Equation 渲染方程
渲染方程在反射方程的基础之上添加了一个自发光项(Emission Term):
\[L_o(p,ω_o)=L_e(p,ω_o)+\int_{Ω^+}L_i(p,ω_i)f_r(p,ω_i,ω_o)(n·ω_i)dω_i\]其中$L_e(p,ω_o)$为自发光项,反射方程中的$cosθ$用$n·ω_i$代替。 (所有光线方向均指向外)
参考对渲染方程的理解: