Blinn-Phong 光照模型
泛光模型
泛光模型只考虑环境光的影响:
\[I_{env} = K_aI_a\]其中$K_a$是物体表面对环境光的反射率,$I_a$是入射环境光的亮度。

这个模型只能得到物体的平面结构,但体现体积感还需要添加下面的漫反射模型。
Lambert漫反射模型
漫反射指的是光从一定角度入射之后,从这个点向四面八方反射,且各方向反射的光的强度相等。
模拟漫反射首先考虑入射光的角度:
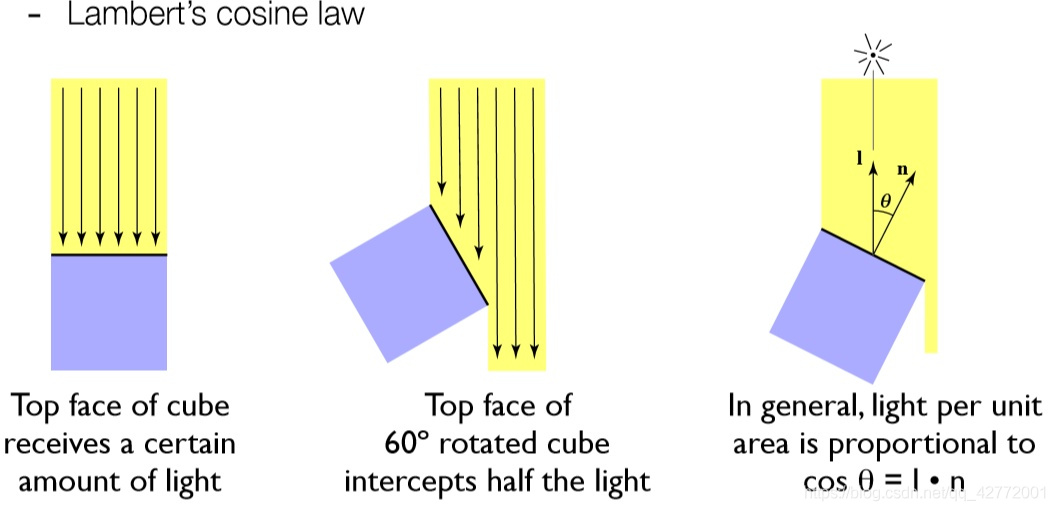
入射角度越倾斜损失的能量越大,应该将光强乘上$cosθ=l·n$,其中$l$是入射光方向,$n$为平面法线方向。
光源与照射点的距离也需要考虑,离得越近强度越大。得到以下公式:
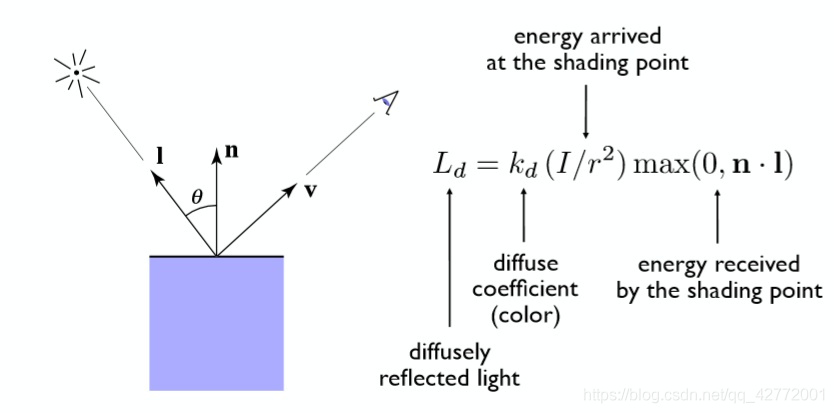
$k_d$为漫反射系数,$I$为入射光强,取max是为了剔除夹角大于90°的光。
将泛光模型和漫反射模型结合,可以得到如下结果:

观察图片,加上高光才会更真实,所以需要用到反射模型。
Phong反射模型
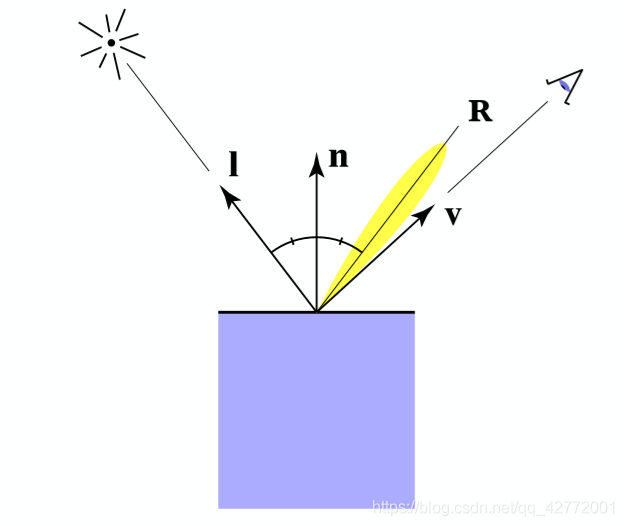
在Phong反射模型中会考虑镜面反射角度$R$与观察角度$v$的夹角:
\[L_s=k_s(I/r^2)max(0,cosα)^p\]其中$k_s$为镜面反射系数,添加指数p的原因是加速衰减。
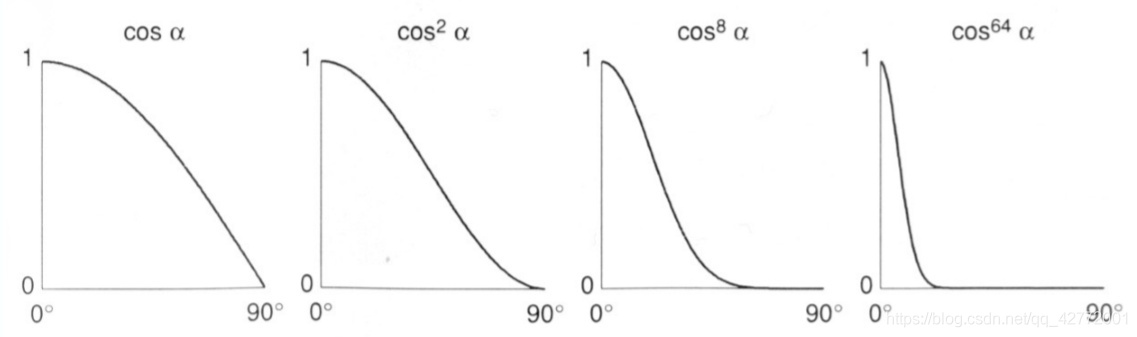
将以上的模型累加得到结果:

对计算反射方向与人眼观察方向角度进行优化,就有了下面的Blinn-Phong反射模型。
Blinn-Phong反射模型
避免计算反射方向$\hat{v}$,为此引入新的矢量:半程向量$\hat{h}$,对$\hat{v}$和$\hat{l}$取平均后再归一化来得到:
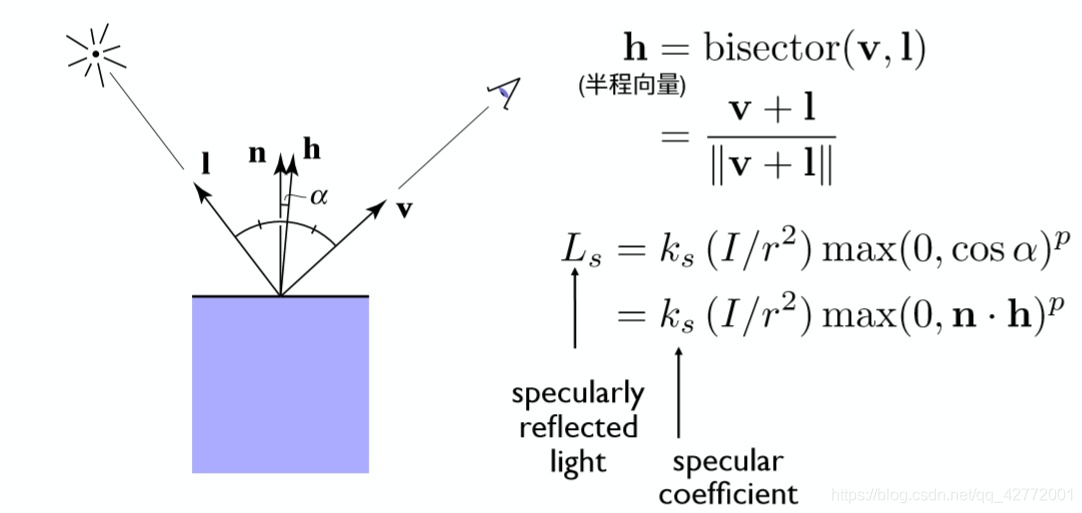
这种方法的优点是加速了角度计算,提升计算的效率,具体来说,算出的近似角度是正确角度的一半。
总结上面的几种光照:

着色方法
在光照模型中涉及法线向量,法线可能对应三角形面,也可能对应顶点。这涉及到了着色频率的问题,可以分类为面着色、顶点着色、像素着色,即是三种不同的着色方法。
Flat Shading
以一个面作为着色单位,利用每个面的法线向量进行一次Blinn-Phong反射光照模型的计算,将颜色赋予整个面,效果如下:

计算很快,但是效果很差。
Gouraud Shading
Gouraud Shading对每个三角形的顶点进行着色,顶点法线计算方法是将所有共享该点的面法线向量相加求均值,再标准化。对于三角形内部的点,利用重心坐标(参考链接)来插值得到它的颜色:
\[c=αc_0+βc_1+γc_2\]$c_0$、$c_1$、$c_2$是三个顶点的颜色,$α$、$β$、$γ$是三角形内一点的重心坐标。

可见对顶点计算,效果有明显提升。
Phong Shading
Phong Shading对上面的方法进行了改进,通过插值法线来真正对每一个点都进行光照模型的计算:
\[n=αn_0+βn_1+γn_2\]得到每个点的法线后,再进行Blinn-Phong模型计算,效果对比如下:

不同精度下的对比:
